Hyperbolic functions are defined in mathematics in a way similar to trigonometric functions. As the name suggests, the graph of a hyperbolic function represents a rectangular hyperbola, and its formula can often be seen in the formulas of a hyperbola. They are defined using a hyperbola instead of a unit circle as in the case of trigonometry. Hyperbolic functions are analogous to trigonometric functions but are derived from a hyperbola as trigonometric functions are derived from a unit circle.
Hyperbolic functions are expressed in terms of the exponential function e x . There are six hyperbolic functions are sinh x, cosh x, tanh x, coth x, sech x, csch x. In this article, we will define these hyperbolic functions and their properties, graphs, identities, derivatives, etc. along with some solved examples.
| 1. | What are Hyperbolic Functions? |
| 2. | Hyperbolic Meaning |
| 3. | Hyperbolic Functions Formulas |
| 4. | Hyperbolic Functions Graphs |
| 5. | Domain and Range of Hyperbolic Functions |
| 6. | Properties of Hyperbolic Functions |
| 7. | Hyperbolic Trig Identities |
| 8. | Differentiation and Integration of Hyperbolic Functions |
| 9. | Inverse Hyperbolic Functions |
| 10. | FAQs on Hyperbolic Functions |
As an ordinary trigonometric function is defined for or on a circle, similarly a hyperbolic function is defined for a hyperbola. In ordinary trigonometry, we were using sine, cosine, and other functions. Similarly, for hyperbolic functions, we use sinh, cosh, tanh, coth, sech, and csch. As in ordinary trigonometric function, we know that the coordinates of points on the unit circle are (cos θ, sin θ), similarly in hyperbolic functions, (cosh θ, sinh θ) forms right half of equilateral hyperbola.
These functions can be solutions of various linear differential equations, cubic equations, and Laplace's equation. The six basic hyperbolic functions are:
Hyperbolic functions are defined analogously to trigonometric functions. We have main six hyperbolic functions, namely sinh x, cosh x, tanh x, coth x, sech x, and cosech x. They can be expressed as a combination of the exponential function. These functions are derived using the hyperbola just like trigonometric functions are derived using the unit circle.
The hyperbolic functions are defined through the algebraic expressions that include the exponential function (e x ) and its inverse exponential functions (e -x ), where e is the Euler’s constant. Let us see all their formulas one by one:
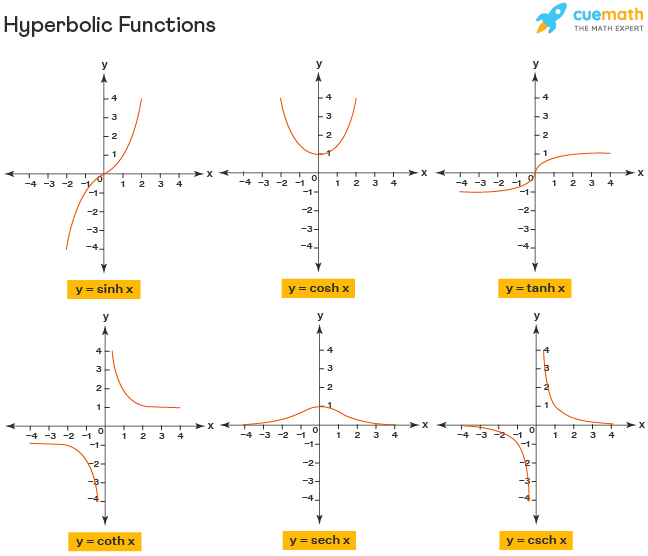
The graph of a hyperbolic function synonymous with its name represents a rectangular hyperbola and its formula can often be seen in the formulas of a hyperbola. Chart of graphs of different hyperbolic functions is given below:

Looking at the graph of a hyperbolic function, we can determine its domain and range. The domains and ranges of these functions are summarized in the following table:
| Hyperbolic Function | Domain | Range |
|---|---|---|
| sinh x | (-∞ , + ∞) | (-∞ , + ∞) |
| cosh x | (-∞ , + ∞) | [1, ∞) |
| tanh x | (-∞ , + ∞) | (-1, 1) |
| coth x | (-∞ , 0) U (0 , + ∞) | (-∞ , - 1) U (1 , +∞) |
| sech x | (-∞ , + ∞) | (0 , 1] |
| csch x | (-∞ , 0) U (0 , +∞) | (-∞ , 0) U (0 , +∞) |
The properties of hyperbolic functions are analogous to the properties of trigonometric functions. Let us go through some of the important properties of these functions which are used to solve various problems in mathematics.
Hyperbolic functions can also be deduced from trigonometric functions with complex arguments:
The hyperbolic trig identities are similar to trigonometric identities and can be understood better from below. Osborn's rule states that trigonometric identities can be converted into hyperbolic trig identities when expanded completely in terms of integral powers of sines and cosines, which includes changing sine to sinh, cosine to cosh. The sign of every term that contains a product of two sinh should be replaced.
The derivative and integral of a hyperbolic function are similar to the derivative and integral of a trigonometric function. Unlike the derivative of trigonometric functions, we can observe the change in sign in the derivative of the hyperbolic secant function. The derivatives and integrals of the hyperbolic functions are summarized in the following table:
| Hyperbolic Function | Derivative | Integral |
|---|---|---|
| sinh x | cosh x | cosh x + C |
| cosh x | sinh x | sinh x + C |
| tanh x | sech 2 x | ln(cosh x) + C |
| coth x | -csch 2 x | ln(sinh x) + C |
| sech x | -sech x. tanh x | arctan(sinh x) + C |
| csch x | -csch x. coth x | ln(tanh (x/2)) + C |
The inverse of a hyperbolic function is called an inverse hyperbolic function. For example, if x = sinh y, then y = sinh -1 x is the inverse of the hyperbolic sine function. The inverse hyperbolic functions expressed in terms of logarithmic functions are shown below:
Important Notes on Hyperbolic Functions
Related Topics
Example 1: Find the value of x if 3 sinh x - 2 cosh x - 2 = 0 using hyperbolic function formula. Solution: We know that sinh x = (e x - e -x )/2 and cosh x = (e x + e -x )/2 Substitute these values in the given equation, we have 3 sinh x - 2 cosh x - 2 = 0 ⇒ 3 [(e x - e -x )/2] - 2 [(e x + e -x )/2] - 2 = 0 ⇒ 3 (e x - e -x ) - 2 (e x + e -x ) - 4 = 0 ⇒ 3 e x - 3 e -x - 2 e x - 2 e -x - 4 = 0 ⇒ e x - 5 e -x - 4 = 0 ⇒ (e x ) 2 - 5 - 4 e x = 0 ⇒ (e x ) 2 - 5 - 5 e x + e x = 0 ⇒ e x (e x + 1) - 5(e x + 1) = 0 ⇒ (e x - 5)(e x + 1) = 0 Since e x ≠ −1, therefore we have e x = 5 ⇒ x = ln 5 Answer: x = ln 5 if 3 sinh x - 2 cosh x - 2 = 0
Example 2: Show that cosh x + sinh x = e x using hyperbolic functions formulas. Solution: We know that sinh x = (e x - e -x )/2 and cosh x = (e x + e -x )/2 LHS = cosh x + sinh x = (e x - e -x )/2 + (e x + e -x )/2 = (e x - e -x + e x + e -x )/2 = 2e x / 2 = e x = RHS Answer: Hence we proved that cosh x + sinh x = e x
Consider LHS = coth 2 x - csch 2 x
= (cosh x/sinh x) 2 - (1/sinh x) 2
= cosh 2 x/sinh 2 x - 1/sinh 2 x
= (cosh 2 x - 1)/sinh 2 x
= sinh 2 x/sinh 2 x --- [Using identity cosh 2 x - sinh 2 x = 1 ⇒ cosh 2 x - 1 = sinh 2 x]
Answer: We have proved the hyperbolic trig identity coth 2 x - csch 2 x = 1.
View Answer >
Become a problem-solving champ using logic, not rules. Learn the why behind math with our certified experts
Hyperbolic functions are defined for a hyperbola. The graph of a hyperbolic function synonymous with its name represents a rectangular hyperbola and the hyperbolic function formula can often be seen in the formulas of a hyperbola. Hyperbolic functions are analogous to trigonometric functions but are derived from a hyperbola as trigonometric functions are derived from a unit circle.
There are six hyperbolic functions, namely:
The formulas for main hyperbolic functions are:
The derivatives of hyperbolic functions are:
The list of inverse hyperbolic functions is:
There are main six hyperbolic functions, namely sinh x, cosh x, tanh x, coth x, sech x, csch x.
The hyperbolic trig identities are formulas of hyperbolic functions which are analogous to trigonometric functions. Some of the hyperbolic trig identities are:
Hyperbolic functions are called hyperbolic because they are derived and defined from a hyperbola just like trigonometric functions are derived from a unit circle. The graph of a hyperbolic function represents a rectangular hyperbola.
The basic difference between trigonometric and hyperbolic functions is that trigonometric functions are defined from a unit circle x 2 + y 2 = 1 and hyperbolic functions are derived from a hyperbola x 2 - y 2 = 1. Another difference between them is that hyperbolic functions are not periodic as trigonometric functions are.